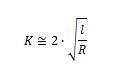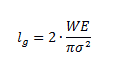The primary function that the fibers have had since their ancient applications, added to the concrete mix, is to counteract the internal tensions that spontaneously trigger in an artifact during hardening or maturation; in this case we refer to auxiliary fibers (otherwise called anti-cracking). The anti-cracking action has been the main application of concrete fibers for centuries. For some time the structural fibers have also been added to the auxiliary fibers, which do not intervene only during the hardening phase of the mixture, but also contribute when the concrete has reached full maturity, improving its performance. In the following paragraphs, for brevity, reference will be made to what was, for various reasons (first of all the chronology), the first function of fibers for concrete, the anti-cracking one, which is common to both auxiliary and structural fibers. These last ones not only have the ability to prevent and stop the cracking phenomenon, but they possess such a robustness that they can also carry more important loads, of a structural nature.
For completeness, we will start by giving an obvious definition: why should fissures and cracks be harmful or simply unwanted? Basically for six main reasons.
- Reduce or compromise the resistance of the product
- Reduce or compromise the “durability” of the product
- Are aesthetically unpleasant
- Can cause water infiltration
- Expose the armor to the action of chemical agents that can affect it
- The thermal insulation capacity of the building is worsening (in the case of a wall)
In the following paragraphs we will explore very easily but nevertheless in a rigorous and exhaustive way, the reasons why any material has certain mechanical characteristics and not others, especially with regard to strength and toughness. Finally, in the case of concrete, it will be demonstrated how the fibers interact with the structure of the cement conglomerate, making it more tenacious and more resistant to brittle fracture.
Genesis of cracks
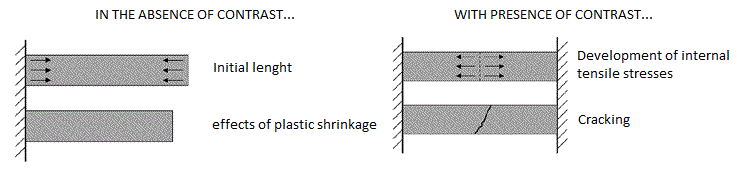
Concrete inevitably tends to develop shrinkage settlements during the fluid/plastic phase (during which the mixture is structurally very weak). Shrinkage, which in the case of concrete products without constraints may not even be such a dangerous phenomenon, necessarily becomes so in the presence of constraints or contrasts, that happens in almost all cases. In fact, shrinkage in the presence of contrast necessarily induces autogenous structural tensions, which if not correctly managed give rise to undesirable effects.
The shrinkage is essentially due to two combined actions: autogenous shrinkage and drying shrinkage, also called hygrometric shrinkage. The first is due to the hydration reaction of the cement, which is a so-called “volume debt” reaction. This means that, in purely volume terms, the sum of the reacting elements is less than the sum of the elements resulting from the reaction. The second effect instead is simply due to the evaporation of the excess of hydration water contained in the fresh concrete (the difference between the total water initially in the mixture and the chemically “combined” water in the hydration reaction). In general, these two different actions are simply said “plastic shrinkage“, they contribute to the same result, which is more accentuated during the first stages of the conglomerate maturation, that is when it is still in the plastic phase, and gradually decreases as maturation is completed.
The effects of autogenous shrinkage are much lower than those of hygrometric shrinkage, so it is possible to approximate the overall plastic shrinkage with drying shrinkage alone. It should be noted that the phenomenon of cracking due to hygrometric causes is certainly not an anomalous fact or an exclusivity of concretes.
The hygrometric plastic shrinkage represents the basic case for which the anti-cracking fibers are used. But the cracks can actually have many other causes besides those self-induced by the concrete itself during maturation. Among these, some can be identified due to the geometry of the laid concrete, others relating to an incorrect design of the structure, and others still due to external factors.
As regards the design causes, they trivially depend on the inadequate prediction of the static and dynamic loads that the concrete work will have to sustain. A structure sized to support certain loads and which would have to bear greater loads could give rise to failures, or in the worst cases to collapses. This is obvious: a road designed to withstand a bicycle will certainly not be able to withstand the transit of a truck! It should be added that in most cases where there are significant design flaws, the cracks are certainly not the main problem.
Among the causes related to geometry, the main ones are the variations in thickness of the section and the presence of edges and wedges. The reason why too marked changes in thickness can cause cracks and fractures, is that in hydraulic binder concretes the hardening takes place from the outside to the inside, so in the case of different thicknesses there would be shrinkage tensions which, in addition to the classic traction effect along the profile of the work, would also produce shear and bending stresses that insist on the internal area still in the plastic phase. Another typical situation in which (if not properly managed) it is possible to find cracks due to the geometry of the work, is in the presence of edges.
The causes due to external factors are innumerable. Among the many we can talk about as an example the incorrect curing of the concrete, the presence of strong temperature changes, the presence of vibrations that are transmitted through the building, the presence of excessive settlements, etc.
Cracking dynamics
What gives fibers this anti-cracking characteristic and why should they help concrete withstand shrinkage stresses? To answer this question, we need to understand what a crack is and what consequences it entails inside a concrete work (as in any other material).
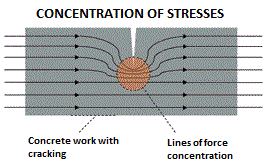
The first and important concept is the concentration of stress at the apex of a fissure, theorized in 1913 by Professor C. E. Inglis. So let’s take the case of a concrete specimen (the concept obviously can be extended to any material) and let us subject it to tensile stresses, such as those generated by shrinkage stresses. The material will be traversed by these tensions along the entire length, moving between the two ends of the specimen. We can schematize the phenomenon as if the body were crossed by lines of flow. In this state, if a fracture is applied to the specimen, one would tend to think that, in correspondence of the defect, the remaining non-cracked section of the material simply takes charge of supporting the tensions that cross it, in a uniform manner. This is completely inaccurate: Inglis theorized that exactly at the apex of the crack (there is even talk of molecular distances) the material is subjected to stresses that are multiplied by several times with respect to the average stresses applied to the specimen.
The multiplication factor (K) theorized by Inglis is approximately equal to:
where l is the length of the crack (or if we want its depth) and R is the radius of the apex.
The precise formula is slightly different from this one and has been theorized for a slit with a spherical or elliptical apex, which is not entirely realistic, although it has been verified experimentally that in reality this formula is an excellent approximation for any other form.
Considering a glass specimen which presents a superficial micro-crack of 2 thousandths of a millimeter in depth and whose radius at the apex is 0.1 millionth of a millimeter (these superficial micro-cracks are not rare at all, they are actually typical in the glass), we will have that for any tensile load applied to the specimen, the material at a certain point will endure up to 200 times more localized stresses !!
A necessary distinction at this point is also between ductile materials (typically metals) and fragile materials (glass, ceramic, concrete, etc.). Ductility is the ability to deform under stress before breaking. This characteristic is also closely linked to the concept of toughness, or the ability of a material to dissipate energy during plastic deformation. One of the main reasons why glass breaks as we know is that being a fragile material, like concrete, in which there are no plastic deformations, a crack always has an extremely small apex radius, whatever its depth.
The multiplication factor therefore becomes high already starting from microscopic cracks. A diamond, though it may be the hardest and most scratch-resistant material known in nature, will shatter with a well-aimed hammering, since it is still a fragile material.
Ductile materials, on the other hand, when subjected to stresses that can undermine the bonds that hold the material together, react by deforming plastically, thus dissipating energy. This property means that in the presence of a crack, the apex will be deformed by the intensification of the stresses, increasing its radius and relieving the concentration of tensions.
You may be wondering: “but then, if it is true that concrete is fragile, why is it still the most used building material “? Acute observation. Very simple: is made to work in compression and not in traction! Or placing it in combination with steel reinforcements, very resistant to traction. Or again, in cases in which it is not possible to do without having stresses in traction with respect to the stresses involved, is mandatory to adopt measures against cracking, firstly by adding fibers to the concrete
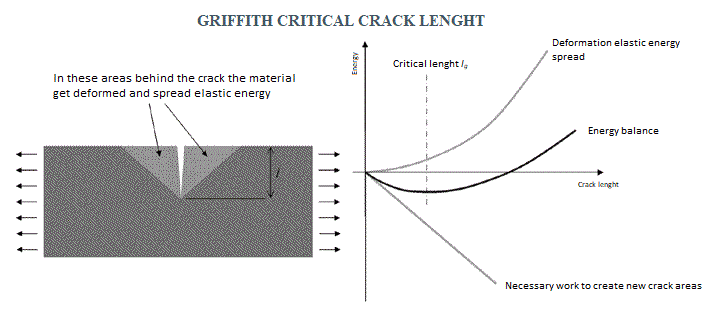
One of the pioneers of fracture mechanics was certainly the engineer AA Griffith, who in 1920 formulated one of the fundamental models of this discipline. Griffith’s stroke of genius was to tackle the cracking dynamics in materials with an energy approach rather than one based on forces and tensions.
He realized that in the phase of propagation of a crack, a so called ‘’fracture work” is done to generate new surfaces and break the molecular and atomic bonds of the material. In the hypothesis of a body that is elastically deforming and in the hypothesis that the effects of the kinetic energy of the fractured parts are negligible, this work of fracture (which absorbs energy) is fed at the expense of the elastic energy stored in the material subjected to traction stress.
From this point of view, therefore, the concentration of Inglis stresses is nothing but a mechanism to transform the energy of deformation into fracture energy, and the condition for a crack to propagate is that the elastic deformation energy per unit of surface is greater than the energy required to form new surfaces.
Going back to analyzing our concrete sample, we note that the areas of it that will release elastic energy are those shown in the figure: two triangles inside the faces of the crack. Griffith noted that the overall area of those triangles varies with the square of the crack length, and therefore also the amount of strain energy released.
On the other hand, fracture work increases in proportion to the fracture length. Translated into practice, this means that for small cracks, crack propagation is an energy-intensive process and does not occur spontaneously. However, once a certain critical length has been overcome, the propagation frees energy which from that moment becomes a spontaneous process, which feeds itself and is therefore brutal.
The critical length is quantitatively defined with this expression:
where W is the fracture work, E the Young’s elastic modulus and “σ” is the tension applied in traction.
Fracture work and elastic modulus are intrinsic properties of the material, while tension is obviously an external factor.
.

Crack stop
So far, we’ve figured out how to create a crack, and we’ve also figured out what the conditions are for its extension into the material. Now let’s see what can be done to stop a crack and make sure that it does not result into a complete breakage of the material, propagating itself in an uncontrolled way.
Let’s start by saying that for a tough material like steel or metals in general, this is quite simple by virtue of a fracture work (W) that is roughly around 10,000 to 1,000,000 J/m².
In these cases, therefore, unlike a fragile material, a crack will have to be quite long (sometimes meters!) In order to rise to spontaneous propagation. In a fragile material, however, the fracture work itself is not very high. Take the case of glass: it is a material that would have an incredibly high theoretical resistance to traction, if it were not that being so dramatically fragile, any infinitesimal fissure (on the surface of the glass there are normally thousands) makes its resistance collapse. Through sophisticated laboratory experiments, it has been shown that extremely thin glass fibers (of the order of a few thousandths of a millimeter) that have almost no cracks have resistances of over 60,000 kg/cm²!!
How is it possible to significantly improve the toughness of a material that is normally very fragile? The answer is suggested by the fiberglass which is a composite material, formed by small glass fibers (catastrophically fragile) immersed in a matrix of hardened resin (slightly less fragile than glass, not by much). So how is it possible to obtain such a tenacious compound, that we can even build boat hulls, simply by combining glass and resin? Well, the answer is in what is called “Cook-Gordon’s trap”.
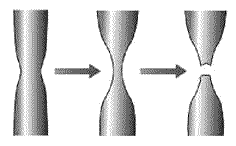
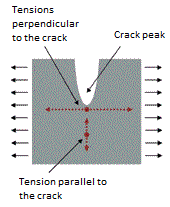
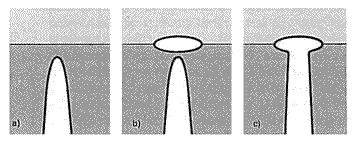
Cook and JE Gordon studied in the 1960s what happened to cracks in a solid composite material. Their attention turned in particular to the crack in propagation when it is about to reach the zone of separation between the two components of the material. They found that, due to a complicated balance of forces in play, at the apex of a crack, not only do we have traction forces in a direction perpendicular to the slit (therefore in the direction of the stress applied to the whole body) which tend to widen further the crack, but there are also tensions in a direction parallel to the crack. The latter are more acute not at the apex but rather slightly below (see the figure), and moreover they are always about a fifth of those perpendicular, in terms of intensity.
Cook and Gordon realized that in a composite material, when the crack in propagation is about to reach the area of separation between the two components of the material, the forces parallel to the slit very often tend to separate the two materials from each other. This mechanism creates a second micro-crack on the path of the main slot; when it propagates further meets the new induced micro-crack (placed perpendicularly to the first), it is trapped. Taking up the formula of Inglis, it is as if now the crack had a much greater radius, and therefore the factor of multiplication of stresses at the apex of the crack collapses abruptly, relieving tensions locally and stopping their propagation.
Fiber action
Now that we have identified causes, dynamics and possible solution for the problem of cracking, the last step is to illustrate how fibers can contribute to improving the mechanical (and not only) performance of concrete works.
First of all, the concrete fibers intervene in the first stage of maturation (up to about 10 hours after installation), when the concrete is still plastic, and the overall shrinkage is more marked. In this context, the cement conglomerate may not have the structural capacity to oppose the tensions generated inside it: cracks and fissures are thus formed. The anti-cracking property of the fibers, therefore, acts in this initial phase, increasing the initial strength of the solidifying conglomerate, intervening even before the cracks are created.
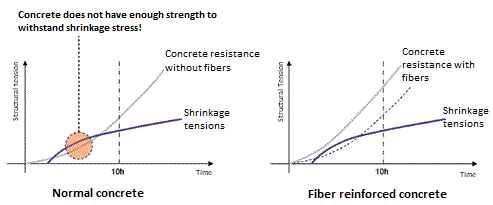
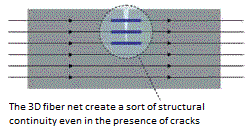
And that’s not all: the 3D lattice created by the fibers, in the case of structural fibers, makes it possible to have a certain resistance even if the concrete had completely fractured, precisely because of the filaments that would pass through the failure capable of supporting limited structural loads (this only for some particular fiber models).
Finally, the fibers have the formidable characteristic of creating many micro-surfaces separating fiber and cement matrix, dispersed throughout the volume of the work and oriented in all directions. In the presence of a crack in propagation (something not infrequently, given the fragile characteristic of the hardened concrete), they go to make up a myriad of small Cook-Gordon traps in the moment in which the crack had to meet the fiber along its way, much often stopping their progress successfully.
It is therefore clear that fibers, even though they certainly cannot be the panacea for all the evils that too often afflict concrete constructions, can contribute to significantly improve some of their characteristics and preventing various intrinsic defects in the material.